再帰を使わない順列生成 : 1から9の数字を1回ずつ使ってできる数を、小さい方から順に列挙する(アルゴリズム編)

1から9の数字を1回ずつ使ってできる数を、小さい方から順に列挙するアルゴリズムです。

次に小さい数を求めるアルゴリズム

ある数Nが与えられたとき、その数に使用されている数字を使用してできる数で、Nの次に大きい数を生成します。

① Nの10^iの桁を、n[i]で表します

②n[i]を桁小さい方からみていき、初めてn[i] < n[i-1]となるiを求めます

③n[0]からn[i-1]まで順番に見ていき、n[i]より初めて大きくなるものを求めます。求めたものをn[j]とします。

④n[i]とn[j]を入れ替えます

⑤n[0]からn[i-1]を逆順にします

この説明だとよくわからないと思うので、具体的な数字でアルゴリズムを確かめてみましょう。

アルゴリズムを適用した例

N=179836542 とします。

① Nの10^iの桁を、n[i]で表します

以下のようになります。

n[0] = 2  // 一の位 (10^0)
n[1] = 4  // 十の位 (10^1)
n[2] = 5  // 百の位 (10^2)
n[3] = 6  // 千の位 (10^3)
n[4] = 3  // 万の位 (10^4)
n[5] = 8  // 十万の位 (10^5)
n[6] = 9  // 百万の位 (10^6)
n[7] = 7  // 千万の位 (10^7)
n[8] = 1  // 億の位 (10^8)

②n[i]を桁小さい方からみていき、初めてn[i] < n[i-1]となるiを求めます

小さい桁から見て行ったとき、3 < 6のとき初めて数が小さくなります。このときn[4] < n[3]なので、i = 4です。

③n[0]からn[i-1]まで順番に見ていき、n[i]より初めて大きくなるものを求めます。求めたものをn[j]とします。

10^4より下の桁で3より大きい数が初めて出てくるのは4です。n[1] = 4なので、j = 1です。

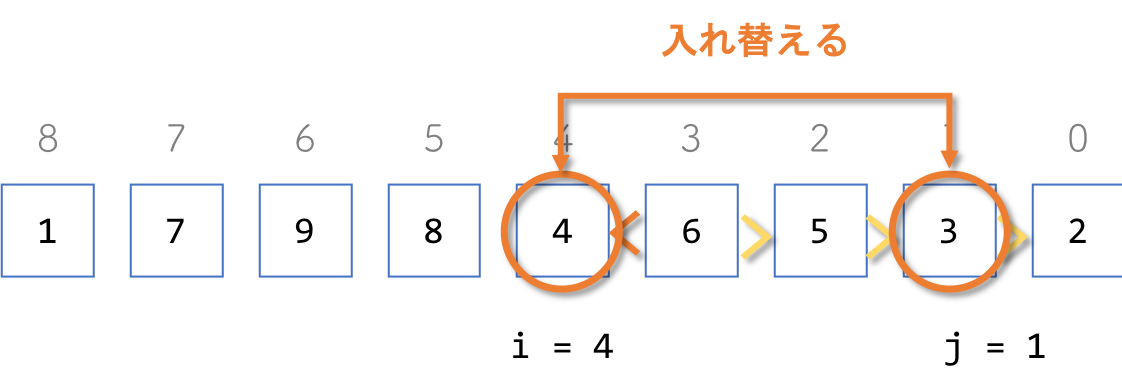
④n[i]とn[j]を入れ替えます

3と4を入れ替えます。入れ替えた後も、n[0]からn[i-1]までは昇順に並んでいますね。

⑤n[0]からn[i-1]を逆順にします

入れ替えた結果です。

以上で、179836542から、次に大きい数である、179842356を得ることができました。

小さい方から列挙するアルゴリズム

1から9の数字を1回ずつ使ってできる数の中で、一番小さい数は123456789です。 ここから、上記アルゴリズムを使用して、次に小さい数を求めます。 さらにそこから得られた数に対して上記アルゴリズムを適用します。

これを繰り返すことによって順列を取り出すことができます。

手順の、

②n[i]を桁小さい方からみていき、初めてn[i] < n[i-1]となるiを求めます

ここで該当するiがなくなったら終了です。

数字が重複しているとき

数が重複しているとき、も上記アルゴリズムはうまく動作します。

例えばN=652331の場合を考えます。

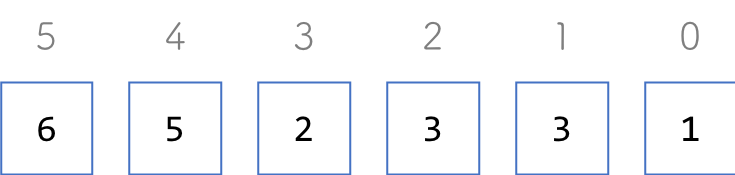
① Nの10^iの桁を、n[i]で表します

②n[i]を桁小さい方からみていき、初めてn[i] < n[i-1]となるiを求めます こちらは上記と同じで、

n[0] = 1  // 一の位 (10^0)
n[1] = 3  // 百の位 (10^2)
n[2] = 3  // 千の位 (10^3)
n[3] = 2  // 万の位 (10^4)
n[4] = 5  // 十万の位 (10^5)
n[5] = 6  // 百万の位 (10^6)

2 < 3のとき初めて数が小さくなります。このときn[3] < n[2]なので、i = 3です。

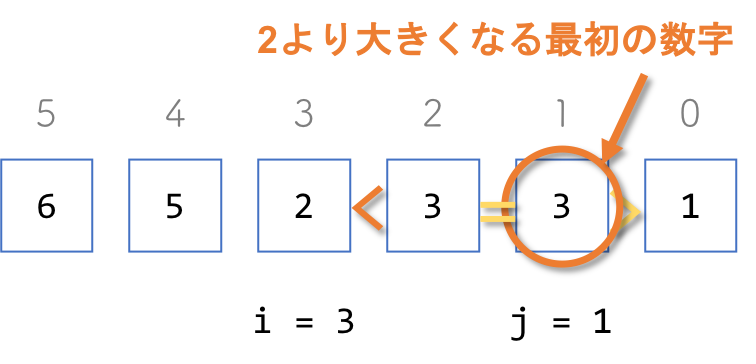
③n[0]からn[i-1]まで順番に見ていき、n[i]より初めて大きくなるものを求めます。求めたものをn[j]とします。

2より下の桁で2より大きい数で、その中で最小なのは3です。3は2つありますが、桁が小さい方を選択します。桁が小さい方は n[1] = 3なので、j = 1です。

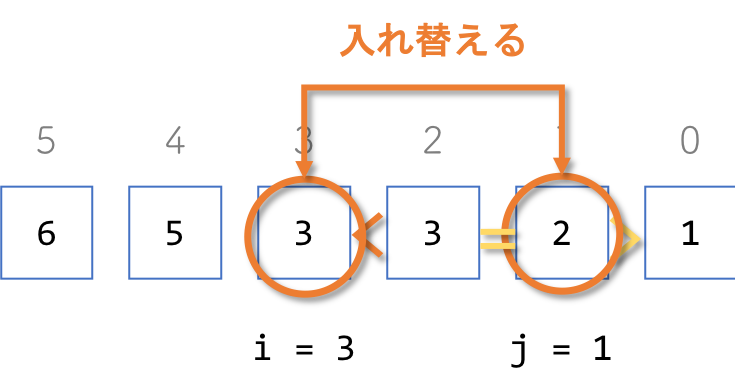
④n[i]とn[j]を入れ替えます 3と2を入れ替えます。

⑤n[0]からn[i-1]を逆順にします

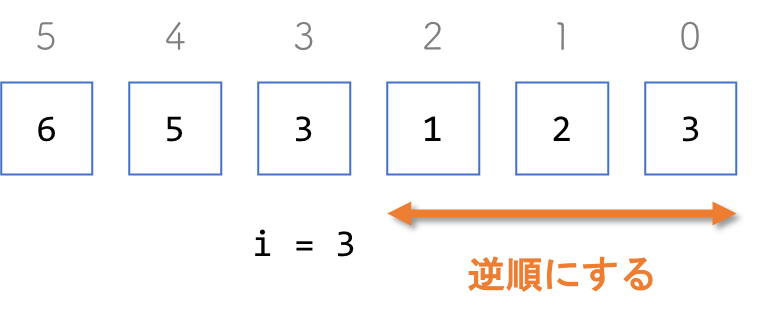
以上で、652331から、次に大きい数である、653123を得ることができました。

応用 : n個の数のうちk個を使用する組み合わせ

上記のアルゴリズムは、n個の数を全て使用する場合の順列を列挙しました。 n個の数のち、k個を使用する場合のアルゴリズムは以下をご覧ください。

★記事作成中